Conversion d'une base décimal
Méthode : De décimal (base10) vers binaire (base2)
Que l'on veuille passer de décimal vers binaire, ou de décimal vers hexadécimal, le raisonnement est fondamentalement le même.
Nous noterons ici b la base de destination, que ce soit binaire, ou hexadécimal.
La méthode la plus simple est celle-ci :
On divise le nombre en base 10 par b.
=> On obtient un quotient q1.
On divise q1 par b.
=> On obtient un quotient q2.
On divise q2 par b.
=> On obtient un quotient q3.
Et ainsi de suite...
Quand le quotient obtenu vaut 0, on cesse les divisions, et on "remonte" dans la liste des restes obtenus, en les écrivant de gauche à droite.
Par exemple, on veut convertir 167 de la base10 -> base2
Les restes obtenus sont alors multiplié par 2
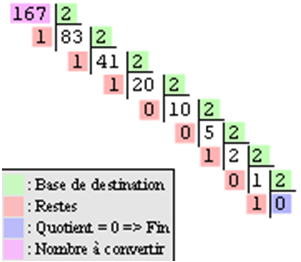
Démarche :
On divise le nombre en base 10 par 2
167 / 2= 83,5
il reste 0,5 que l'on multiplie par 2 soit 1(2)
83 / 2 = 41
il reste 0,6875 que l'on multiplie par 2 soit 1(2)
41 / 2 = 20
il reste 0 que l'on multiplie par 2 soit 0(2)
et ainsi de suite
On obtient à la fin 167(10) = 1010 0111(2)
Méthode : De décimal (base10) vers hexadécimal (base16)
Convertissons à présent 689 de la base 10 -> base 16
L'organisation de la succession de divisions est la même que pour le premier exemple
Les restes obtenus sont alors multiplié par 16 puis convertis dans leur équivalent hexadécimal.
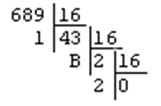
Démarche :
On divise le nombre en base 10 par 16
689 / 16 = 43,0625
il reste 0,0625 que l'on multiplie par 16 soit 1 (base10) à convertir en hexadécimal 1 (base16)
43/19 = 2,6875
il reste 0,6875 que l'on multiplie par 16 soit 11(base10) à convertir en hexadécimal B (base16)
2/16 = 0,125
il reste 0,125 que l'on multiplie par 16 soit 12(base10) à convertir en hexadécimal 2 (base16)
On a donc: 689(10) = 2B1(16)