Notions de bases numériques
Fondamental :
En général, on désigne sous le terme de "Base n" la base qui utilise les chiffres de 0 à n-1.
Par exemple, nous utilisons quotidiennement la base 10, aussi appelée décimale, qui utilise les chiffres de 0 à 9.
3 types de base numériques : Les bases 2 (binaire), 10 (décimal), et 16 (hexadécimal).
Base décimale (base10) ou Base (10)
La base 10 est reconnue car c'est elle que nous avons l'habitude de manipuler
Ce système est basé sur une logique à dix symboles, de 0 à 9, avec une unité supérieure (dizaine, centaine, etc.) .
Base binaire (base 2) ou Base (2)
La base 2, c'est la plus proche de la machine
L'unité élémentaire ne peut prendre que les valeurs 0 et 1, s'appelle un bit (de l'anglais binary digit). Une suite de huit bits s'appelle un octet.
Base hexadécimal (base 16) ou Base (16)
La base 16 est employée pour minimiser le nombre d'erreurs à la lecture et à l'écriture par rapport à la base 2 (car 4 chiffres binaires correspondent à un chiffre hexadécimal). Souvent utilisée dans la communication entre machine.
En base 16, puisque notre alphabet ne comporte pas 16 chiffres, nous utilisons les dix chiffres usuels, soit de 0 à 9, puis les six premières lettres, soit de A à F.
Savoir différencier une base d'une autre est certes utile, mais il peut être quasiment indispensable de passer de l'une à l'autre.
Voici un tableau de correspondance :
Exemple : Écriture décimale (base10)
2022 en base décimale pourra s'écrire 2022(10)
1010 en base décimale pourra s'écrire 1010(10), si on ne précise pas la base, il est impossible de savoir si c'est une valeur décimal ou binaire
Exemple : Écriture binaire (base2)
Écriture binaire :
1010(2)
0111(2)
Précision :
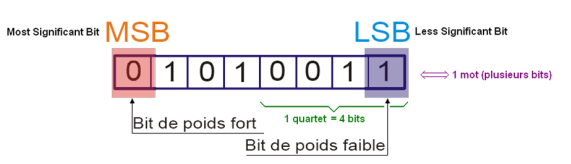
Exemple : Écriture hexadécimal (base16)
Écriture hexadécimal :
1B2(16)
2022(16) n'as pas la même valeur que 2022(10)
1010(16) n'as pas la même valeur que 1010(2)
